實作 Bresenham 直線演算法

這次要玩的是比較軟體一點的東西：Bresenham's line algorithm
Wiki 上的中文翻譯是 "布雷森漢姆直線演算法"
這原本是圖學在用的, 在研究 3D 印表機的韌體時注意到註解裡有寫這
才發現原來它也可以拿去用在機械控制上
對於 3D 印表機來說這是非常重要的核心程式
準確的一邊走一邊擠出適量的料, 這機器絕大多數的工作時間都是在做這
而實現這動作的程式就是布雷森漢姆直線演算法
我所拿到的印表機韌體在這裡寫了非常多的程式, 就為了能讓它安分的走直線
所以我把它研究了一下, 然後重新寫成自己的版本給新玩具使用
這演算法的精神在 wiki 上已經寫得很詳細了, 都是中文字
我不認為有必要再重複, 所以只紀錄應用時的小修正



在我的程式中比較不同的是我寫的是可以同時控制四軸的直線算法
考慮原先 wiki 上的兩軸算法, 我們會先找出較長的軸, 以它為基準
選長軸的理由是當長軸每走一步時, 短軸最多只走一步, 所以我們可以用斜率去累加判斷
如果用短軸為基準, 短軸每走一步可能長軸會走三步, 這樣我們會需要去計算要多幾步出來, 很麻煩
如果總是選長軸我們可以保證短軸最多同時要走一步, 不須去算要多走幾步
而用到多軸時玩法依然是相同的, 假設四軸都要走
那我們就從四軸中找出最長的那一軸, 然後以它為基準
接著去和另外三軸分別求斜率, 我們不要去管它到底是 X 還是 Y, 就很單純的一對一算
所以我們應該會得到三個斜率值, 接著以最長軸為基準開始走, 每走一步就分別對另外三軸累加斜率
累加超過 0.5 就讓它走一步, 然後累進值減去 1, 每一軸都這樣做, 這樣就是四軸演算法
計算時千萬不要試圖用三度空間去思考它, 這樣會爆炸XD
這讓我想起以前學線性代數時腦袋爆炸的情況(?)
兩軸是一對一, 三軸一對二, 四軸一對三, 就這樣！空間中在什麼位置不重要

我的程式也有做 wiki 上寫的最佳化部份, 也就是全部整數計算
轉換過程如下, 這是原來的算法的部份算式 (取自 wiki)

    real error := 0
    real deltaerr := deltay / deltax
    for x from x0 to x1
        error := error + deltaerr
        if error ≥ 0.5 then
            y := y + ystep
            error := error - 1.0

wiki 版有 swap(x0, y0) 這選長軸判斷, 這裡我們用 loop 去比較所以沒有 swap
另外由於步進馬達控制器有旋轉方向的設定, 換轉動方向等同加減變換
所以我們也不需要這行：

if y0 < y1 then ystep := 1 else ystep := -1

不用考慮短軸要遞增還是遞減, 對馬達控制器設定方向後永遠用加的, 即 ystep 永遠是 1
最佳化第一階段是消除浮點數, 我們可以把 error 的算式同乘 deltax
於是變成這樣：

    real error := 0
    real deltaerr := deltay
    for x from x0 to x1
        error := error + deltaerr
        if error ≥ (deltax * 0.5) then
            y := y + ystep
            error := error - deltax

error 算式用來評估是否讓短軸多走一步, 它只是一個評估指標
和實際走步數的算式是分開的, 修改它並不會影響實際步數
這改進可以避免循環誤差, 因為浮點數精度有限, 總是用浮點數的斜率去累加會不斷產生誤差

當 error ≥ (deltax * 0.5) 這裡會有效率考量, 因為計算結果是浮點數, 浮點數比較會慢些
為了完全整數化, 我們再修改算式, error 原本是從 0 開始, 把起始點升到 deltax * 0.5
讓 error 變化量由 (-0.5 * deltax) ~ (0.5 * deltax) 改為 0 ~ deltax
於是變成這樣

    real error := deltax * 0.5
    real deltaerr := deltay
    for x from x0 to x1
        error := error + deltaerr
        if error ≥ deltax then
            y := y + ystep
            error := error - deltax

不過這改進效果較小, 因為我們可以用整數去存浮點數算出的結果
原先的 deltax * 0.5 只是用來比較用, 它並不參與累加, 不會貢獻誤差
用整數去存它並不會造成損失

別人寫的韌體也是有做最佳化, 所以如果不看註解只看程式會完全搞不懂為什麼這樣加
因為只看程式並沒有辦法和斜率聯想在一起, 自然是感到莫名其妙

接著是 demo, 這是這次演算法驗證用的機器


背面的樣子：

它是做啥用的先別理它, 還在開發階段的玩具, 無法保證能成功
有成功就會再有文章說明 (雖然有玩過類似設備的一看就知道這啥XD)
它有三個軸, 每個軸都有一顆步進馬達轉動
控制板為 3D 印表機在用的 Melzi Ardentissimo, Google 可找到電路圖
雖然是 XYZ 軸但是我接到板上是接 XYE, 這張板上的 Z 軸部份電路似乎有些問題...
控制馬達的 IC 是 A4988, 其控制細節可參考前篇 用 A4988 控制步進馬達
設定為 1/8 micro step, 也就是對 A4988 送 8 個 clock 就等同馬達實際走一步
馬達的精度為 1.8 度, 即馬達的一步是轉動 1.8 度, 走 200 步即一圈
所以若要讓螺桿轉一圈, 我們要送 8 * 200 = 1600 個 clock 給 A4988
從上圖可以看到馬達轉動的是螺桿, 這是 3D 印表機常用於 Z 軸的規格, M8 螺桿
螺紋的間距 (pitch) 為 1.25mm, 間距代表的位置如下圖

上圖是一根螺桿, 箭頭指的兩垂直線間的距離就是間距, M8 螺桿是 1.25mm
若在螺桿上鎖上螺帽, 固定螺帽後將螺桿轉一圈, 螺帽便會移動 1.25mm
對 A4988 的控制就是每送 1600 個 clock 就等同移動 1.25mm

接著把我的控制板接上電腦, 用 ubuntu 上的 minicom 連接, 關閉硬體流量控制
速度設定為 38400bps 8N1, 然後輸入下面這幾行 G code (自訂的, 非標準！)

g0 e-5
g0 y20
g0 x20
g0 y-20
g0 x-20
g0 e5

這幾句的意思是 E 軸走 -5 mm (Z 軸電路故障所以換接 E 軸, 請把 E 軸當 Z 軸就是了)
Y 軸走 20mm, X 軸走 20mm, Y 軸走 -20mm, X 軸走 -20mm, E 軸走 5mm
我在移動架上用膠帶黏了一枝筆, 移動 Z 軸就是把筆往下移動到紙上
所以上面這些指令下完後可以得到一個正方形, 然後下面這裡有另一組 G code

g0 e-5
g0 y40
g0 x20 y-20
g0 y-20 x-20
g0 e5

這可以畫三角形, 實驗結果：

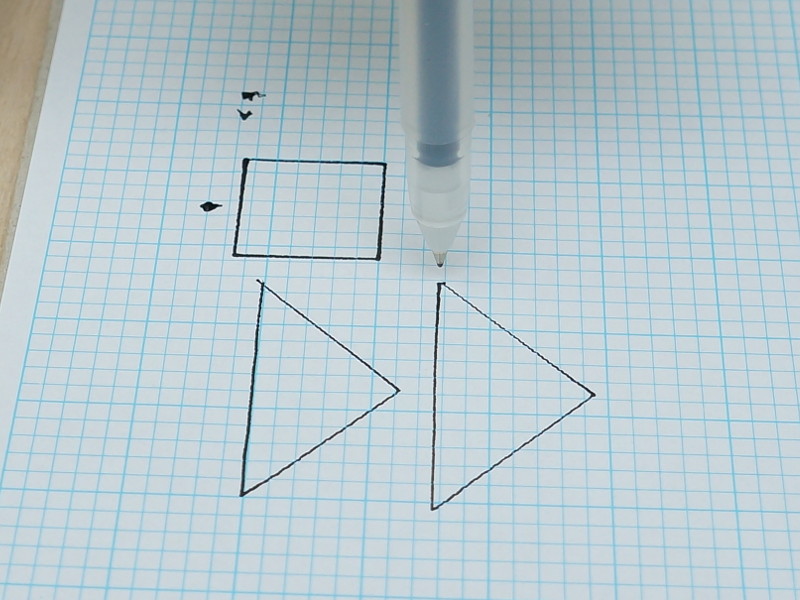
三角形有兩個, 左側的是只靠膠帶固定的, 右側的是用手壓著筆的
只用膠帶不太穩, 所以畫出來歪歪的, 手壓固定後看起來還行, 畫完後都能回到原位沒有太大偏差
這裡附上本機韌體原始碼供參考：

Melzi.zip

由於這張板子有點問題, 之後會換掉, 換成別家一樣用 A4988 的板子
我想之前會需要用手動將 Z 軸歸零應該是硬體問題